This web page was produced as an assignment for an undergraduate course at Davidson College.
Click to see the paper "Synthetic Gene Networks That Count" (Friedland et al., 2009)
All of the following summaries, opinions, ideas, and table/figures are based off of the paper (Friedland et al., 2009).
____________________________
Paper Summary
I was used to learning about relatively simple, straight-forward manipulations to biological systems not dependent on sequential steps; however, this paper illustrated that manipulations in the form of synthetic biological counters are an intensive process involving different elements to work together to count in order. This synthetic biology paper taught me much about how biological counter systems work in general. Specifically, I learned how a biological counter is designed like a circuit, and how counters use preexisting transcription/translation mechanisms to count, and that various inputs or inducers to the counter controls when counting occurs. I learned how each count in counter models represents a specific event occurring, such as a protein being produced at a specific count. Successful counting by the counter can be also be confirmed by having the produced protein being GFP, which has detectable fluorescence.
I learned that predictions made based off counter models need to be validated by placing the synthetic counters must be transformed into cells to see how well and versatile the counters operate in different treatments. Initially, I assumed the counter models would not have distinct counting due to uncontrollable, random cellular factors affecting counter function. However, I was surprised that the experimental results for the most part confirmed the predicted counting function by the counters. Counting has also been shown to work reliably even if the inducer (i.e. arabinose pulse) of the counter has varied length and frequency. The synthetic counter model does not perfectly predict all possible variation since the data shows minor unintended counting/leakages occurring; overall, the model predictions of counting were still confirmed by the results. Beyond the counters presented in this paper, the paper also taught me that counters have potential for more complexity, and can serve a variety of other purposes. For example, counters can designed to count by taking advantage of certain cellular elements (for example, a biological pathway) in order to assist research. After counting a determined number of times, counters can also be used to produce a specific protein of interest that may serve a beneficial research or medical purpose.
Paper Opinion
Each of the four figures had strengths and weaknesses, but were essential to understanding counter mechanisms and supporting data. I appreciated how figure 1 spent more time explaining the mechanics to both RTC two- and three-counter in order to familiarize the reader with the topic. Figure 2a and 2b were initially confusing since the dots and lines are not labeled as to whether they represent experimental results or mathematical modeling; however, I deduced that the solid circles indicated the actual experimental data using the two-counter because it is closer to the experimental results shown in figure 1b. I would have been preferred a short explanation as to what the dots and lines represented in the legend of figure 2a and 2b. Curiously, the legend for figure 2c and 2d explains the meanings of the dots and lines. I liked how figure 3, in contrast to counter description in figure 1, assumes that the reader has a basic understanding and devotes space only to the more complicated DIC three-counter. I was not sure why two different graph types (two-dimensional graph in figure 2 and the three-dimensional graph in figure 3) were needed to show the same kinds of data comparing the effects of pulse interval and duration on fluorescence, but the three-dimensional graph in figure 3 may have been used to save some space. I am not sure why the flow cytometry data of figure 4c includes a control, but the flow cytometry data of figure 4d does not include a control, which makes it difficult to determine what the background fluorescence is for figure 4d.
Some thoughts I had spanned across several figures. The circuit diagrams of the counters in the figures 1, 3, and 4 were initially intimidating due to the many circuitry components, symbols, and names. Fortunately, the paper text was very helpful in explaining and supplementing the detailed figures. I appreciated that the colors representing different cell population treatments were kept consistent across figures 1 and 2, and also within figures 3 and 4. The presentation of flow cytometry data was slightly different in figures 1, 3, and 4, which did not make sense since each form did not appear to offer any significant benefits or advantages over the other forms.
Despite some room for improvement, the paper did very good job in using both figures and text to describe the counters and data. The amount of data displayed in the figures helped me to more likely believe that the experiments show the validity of the counter designs. The paper was challenging in some places since I was not accustomed to thinking in terms of circuits, but the authors did a good job in making the potentially confusing topic comprehensible to readers. The paper also made the concept of biological counters very appealing to readers by noting that counters are validated and have much potential for use.
____________________________
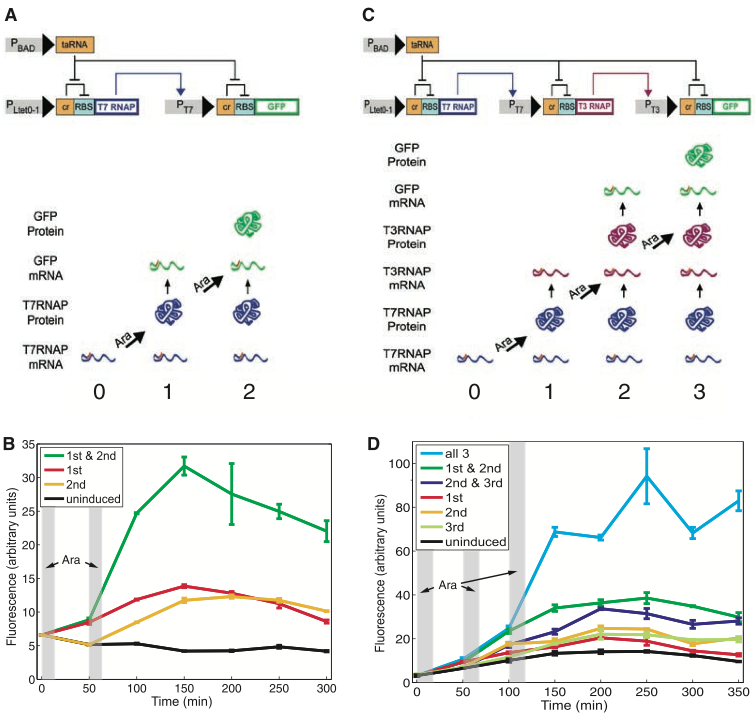
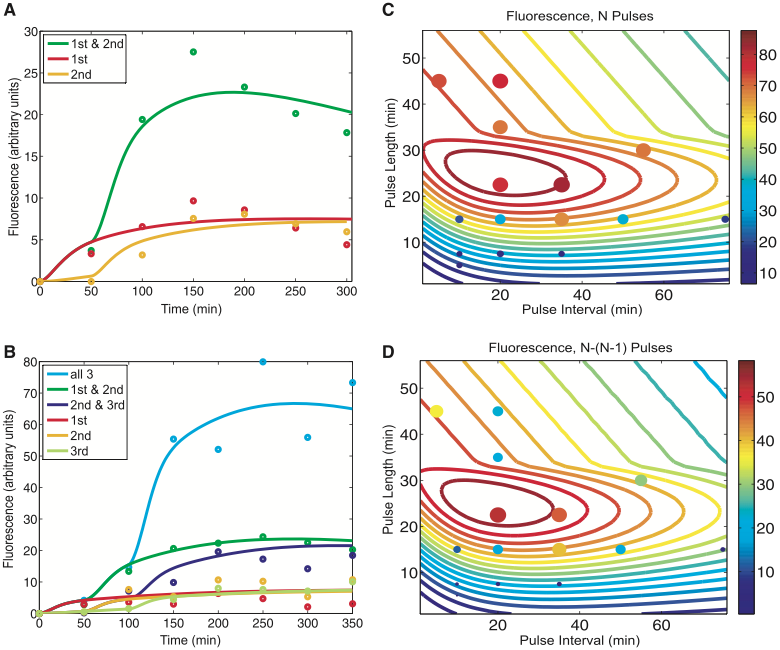
Figure 1 introduces and demonstrates the first of two synthetic counter types, which is the RTC (riboregulated transcriptional cascade) two- and three-counter. After introducing the RTC counter models in figure 1a and 1c, the authors use experimental data from cells containing the RTC counter to confirm the models in figure 1b and 1d.
Figure 1a shows the circuit model of the RTC two-counter and what happens as it counts to two. At the beginning, the constitutive promoter PLtet0-1 facilitates T7 RNAP (RNA polymerase) transcription; after transcription, the cis-repressor RNA sequence (cr) forms a hairpin to the complimentary RBS (ribosome-binding site) sequence, which prevents the ribosome from binding and translating T7 RNAP. However, the first arabinose pulse activates PBAD (arabinose promoter), which facilitates transcription of the downstream taRNA (transactivating RNA). As a result of taRNA binding to cr and thus blocking cr interaction with RBS, the ribosome is able to bind to the RBS and translate T7 RNAP mRNA into T7 RNAP protein, which represents the counter counting to one. Removing arabinose, taRNA and stopping further T7 RNAP protein production after the first pulse ideally prevents the counter from prematurely continuing to count. The already produced T7 RNAP protein from the first count binds to the PT7 promoter, which facilitates GFP transcription to mRNA. After GFP transcription however, cr binds to RBS, which blocks ribosomes from translating GFP mRNA to protein. When a second pulse of arabinose activates PBAD, PBAD can facilitate taRNA transcription, so that taRNA binds to cr, preventing cr from binding to RBS, which allows for the ribosome to translate GFP mRNA to protein. The production of GFP protein, which is measured by fluorescence, represents the counter counting to two.
Figure 1b flow cytometry data shows the averaged fluorescence levels over time from three replicates of transformed E. coli cell populations with the RTC two-counter. The transparent vertical grey bars represent when the arabinose pulses took place. The RTC counter was noted to count over a shorter time frame (five to six hours) compared to the DIC counter (25 to 40 hours) described in figures 3 and 4. Because GFP protein should only be expressed after both the first and second pulse of arabinose, there should not be considerable increase in expressed fluorescence with cells receiving one or no arabinose pulse. The uninduced cells (black line) are the control receiving no arabinose, which represents the background fluorescence rate. The cells receiving two pulses of arabinose (green line) were able to successfully count to two by having intended GFP protein expression, illustrated by the substantial increase in fluorescence after the second grey bar. The other two lines (cells receiving either the first (red line) or second (yellow line) pulse only) represent treatments where there should ideally be no increased fluorescence since the insufficient pulses given to the cell would not allow the counter to count to two with GFP protein expression. Even though these cells did not receive both arabinose pulses to count to two, the graph shows these cell populations having small increased fluorescence (much lower than the cells receiving both pulses), indicating unintended GFP protein production due to leakage. The leakage resulted from uncertainty and variation regarding the model and cell.
Figure 1c is similar to what was depicted in figure 1a; this part of figure 1 demonstrates the RTC three-counter circuit model and what events occur as the counter counts to three. Due to the first arabinose pulse causing taRNA to remove repression of T7 RNAP translation, the RTC three-counter can produce T7 RNAP protein in its first count. The T7 RNAP protein then binds to the PT7 promoter, which facilitates T3 RNAP transcription. As previously described, cr inhibits T3 RNAP translation until the second arabinose pulse, which causes taRNA to remove cr inhibition of translation, allowing for T3 RNAP protein production. The T3 RNAP protein can then bind to the PT3 promoter, which facilitates GFP transcription. Again, cr prevents GFP translation until the third pulse is given, which causes taRNA to remove cr inhibition, allowing translation and GFP protein production. GFP production (increase in fluorescence expression) can be used to confirm that the RTC three-counter can count to three.
Figure 1d is similar to figure 1b in showing flow cytometry data of the averaged fluorescence over time from three replicates of transformed E. coli cell populations, with cells containing the RTC three-counter. The transparent vertical grey bars represent when the arabinose pulses took place. Because GFP protein should only be expressed after all three pulses of arabinose, there should not be considerable increase in expressed fluorescence with cells receiving one, two, or no arabinose pulse. The uninduced cells (black line) are the control receiving no arabinose, which represents the background fluorescence rate. Cells receiving all three pulses of arabinose (light blue line) were able to successfully count to three by having intended GFP protein expression, illustrated by the substantial increase in fluorescence after the third grey bar. The other cells receiving only one pulse (either the first pulse (red line), second pulse (yellow line), or the third pulse (light green line)) had little increased fluorescence expression over time, close to the control fluorescence expression. Cells receiving the first and second pulses (dark green line), or the second and third pulses (dark purple line) show a little more increased fluorescence (compared to the cells receiving only one pulse), but the fluorescence levels were still much lower than the fluorescence levels of the cells receiving all three pulses. Cells that do not receive all three pulses should ideally have no increased fluorescence since insufficient pulses given to the cell would not allow the counter to count to three with GFP protein production, but the graph shows minor fluorescence level increases in these cells as a result of leakage.
Overall, figure 1 goes through a detailed step by step process of how the counter works, and shows that the RTC counter works using experimental results that illustrate that in most cases when the correct number of arabinose pulses are given, the RTC counter counts correctly.
___________________________

Fig. 2. Modeling predictions and RTC three-counter experimental characterization (Friedland et at., 2009).
Figure 2 shows more validation of the RTC two-counter and three-counter from figure 1 by comparing the experimental data against mathematical modeling predictions for the RTC counters in different circumstances.
Figure 2a depicts how well the experimental results of the RTC two-counter agree with the mathematical model (used to predict the results of the RTC two-counter). Fluorescence is graphed as a function of time, with each color representing different arabinose pulse treatments on cells, dots representing experimental results, and lines representing predictions by the mathematical model. The results show cells receiving either the first pulse (red circles) or second pulse (yellow circles) had relatively little increase in fluorescence over time. Cells receiving both pulses (green circles) had a relatively bigger increase in fluorescence over time. The mathematical modeling for cells receiving either the first pulse (red line) and second pulse (yellow line), along with cells receiving both pulses (green line) seems to be relatively close to their corresponding experimental result circles.
Figure 2b is similar to figure 2a, but instead depicts how well the experimental results of the RTC three-counter agree with the mathematical model (used to predict what the experimental results of the RTC three-counter). Fluorescence is graphed as a function of time, with each color representing different arabinose pulse treatments on cells, dots representing experimental results, and lines representing predictions by the mathematical model. The results show cells receiving either the first pulse (red circles), second pulse (yellow circles), or the third pulse (light green circles) had little fluorescence increase over time. The results of cells receiving two of the three possible pulses, either the first and second pulses (dark green circles), or the second and third pulses (dark purple circles), show that there was a little increase in fluorescence (compared to the cells receiving only one pulse), but the fluorescence levels were still lower than the fluorescence levels of the cells receiving all three pulses. Cells receiving all three pulses (light blue circles) had a relatively bigger increase in fluorescence over time. The mathematical model lines for the most part closely aligned to the corresponding color dots, with some variations in the experimental results not accounted for by the model.
The results from both figure 2a and 2b indicate that the mathematical models for both the RTC two-counter and three-counter mostly match with the experimental results of the respective counters. The results provide more evidence that the theoretical counter models shown in figure 1 can predict fairly well when an increase in fluorescence should occur due to the transcriptional/translational processes of the synthetic counter.
Figure 2c and 2d further tests how well the mathematical modeling could predict fluorescence when the pulses were varied by length and frequency. Only the RTC three-counter in cells is considered for these two panels of figure 2.
Figure 2c shows the predicted and actual fluorescence levels after three pulses of arabinose. The counter lines represent the mathematical modeling predictions of fluorescence levels produced by the RTC three-counter, where colors closer to red represent higher fluorescence while colors closer to blue represent lower fluorescence. The actual experimental pulses are depicted as circles, with fluorescence expression levels represented by circle sizes and color (same color-coding as the contour lines). The model predictions matched well with experimental results of fluorescence at different pulse length/interval combinations, indicating that the RTC three-counter counts well over a range of different pulse lengths and intervals. The contour lines indicates that the most optimal counting by the RTC three-counter (highest fluorescence when the counter was most efficient in producing the most GFP) occurs at pulse lengths of 20-30 minutes and pulse intervals of 10-40 minutes. However, at more extreme pulse lengths/intervals (towards the graph periphery), the counting of the RTC three-counter was not as good, indicated by lower fluorescence at these areas.
Figure 2d is similar to format to figure 2c, except that the fluorescence displayed here is the difference in fluorescence between the second and third pulses. The color-coded contour lines (based off mathematical modeling) and circles (based off experimental results) still mostly reflect the overall trends of contour lines and circles seen in figure 2c. The contour lines here also match up fairly well with the circles, indicating that the RTC three-counter was able to count well for many combinations of pulse length and intervals. The optimal level of the RTC three-counter was also found in the similar area for figure 2c. Similarly to figure 2c, counting was not as good at the extremes of pulse lengths/intervals as seen by the lower fluorescence at these areas.
The results from both figure 2c and 2d show that the RTC three-counter can count over a range of pulse length/intervals, illustrated by the contour lines corresponding to circles of similar fluorescence. Higher fluorescence indicate optimal combinations of pulse length and pulse interval while lower fluorescence indicate less than optimal combinations of pulse lengths and intervals. The authors indicate that the less than optimal counting by the model with some pulse lengths/intervals are due to unpredictable, random cellular elements.
Overall, figure 2 shows that the experimental results mostly support the mathematical modeling predictions for the RTC three-counter, and the counter can work over a certain range of pulse lengths/intervals.
____________________________

Figure 3 describes the second constructed synthetic counter: DIC (DNA invertase cascade) counter; similar to what figures 1 and 2 described about the RTC counter, figure 3 demonstrates that the DIC counter model works because of experimental validation.
Figure 3a is the circuit model of the DIC three-counter, with three counting units in order to count to three. The first and second SIMM (single invertase memory module) contain recombinase recognition sites (at both ends) where recombinase binds to to flip the SIMM, an inverted PBAD promoter, RBS (ribosome binding site), recombinase gene that produces enzymes that flip the SIMM, ssrA tag that degrades recombinase in order to prevent unintended flipping of the SIMM, and Term that prevents unintended transcription from continuing on to the next SIMM. At the beginning, the first PBAD is orientated in the right direction for the correct transcription of the first SIMM downstream. The first arabinose pulse activates the first PBAD, which facilitates transcription of only the first SIMM, including the recombinase Flipe. After translation, Flipe recombinase protein is produced and binds to the FRTf and FRTr recombinase recognition sites on either side of the first SIMM. The result is an inverted SIMM (between the two FRT sites), so Flipe cannot be translated to protein anymore since it faces the wrong direction. The inversion also inverts the inverted promoter PBAD within the SIMM, so it is now in the right location and direction to facilitate transcription of the second SIMM. Instead of Flipe and FRT in the second SIMM, cre is the recombinase and loxPf and loxPr are the recombinase recognition sites of the second SIMM. When the second pulse is given, the correctly facing PBAD in the first SIMM is activated and facilitates transcription of the second SIMM. When translation produces Cre protein, Cre binds to loxPf and loxPr, which inverts the second SIMM in between the two loxPf sites. As a result, the previously inverted PBAD in the second SIMM is now inverted to the right place and direction to facilitate transcription of the third SIMM. Instead of a recombinase gene, the third SIMM has a GFP gene. When the third pulse is given, PBAD is activated and facilitates transcription of the second SIMM. Subsequent translation produces GFP protein, which is detected as fluorescence and confirms that the DIC three-counter was able to count to three.
Figure 3b is similar to the type of data shown in figure 1b and 1d, except the graph displays only DIC three-counter cells receiving all three pulses. The flow cytometry data shows the averaged fluorescence levels over time from three replicates of transformed E. coli cell populations with the DIC three-counter. Fluorescence is graphed as a function of time, with the three grey vertical bars representing when the arabinose pulses took place. The DIC counter was noted to count over a longer time frame (25 to 40 hours) compared to the RTC counter (five to six hours) described in figures 1 and 2. There should not be a considerable increase in fluorescence during the first pulse since the promoter for the third SIMM is still inverted, so no transcription and translation can occur for GFP yet. No increase in fluorescence should occur due to the second pulse because an additional pulse arabinose is needed to activate the promoter for the third SIMM before GFP can be produced. Fluorescence should increase in the third pulse because the promoter for the third SIMM is activated and GFP production can occur. The data shows that the DIC three-counter cells can count because fluorescence is expressed much more during the third pulse. Leakage in the counter allowed for a small amount of unintended fluorescence expression before the counter reached three.
Figure 3c compares the effect of pulse duration and intervals on the DIC three-counter, like in figures 2c and 2d, except that figure 3c utilizes a three-dimensional graph. The x and y axis represent various arabinose pulse lengths and pulse intervals. The z axis represents fluorescence ratio between a DIC three-counter cell population receiving three pulses and a DIC three-counter cell population receiving only two pulses. The color-coded grid (corresponding to fluorescence) was calculated by the mathematical model, and the black circles on the grid represent experimental results. Since the fluorescence ratio is around 1.5 for most pulse intervals and lengths, this indicates that the DIC three-counter cell population receiving three pulses expressed more fluorescence compared to the cell population receiving only two pulses. The DIC three-counter cells require three pulses in order to count to three and express more GFP, compared to the DIC three-counter cells given only two pulses, which should express less GFP expression since these counters could not count to three. In addition, the mostly consistent ratio of 1.5 indicates that the DIC three-counter was able to count properly over a range of different pulse lengths and intervals.
Overall, figure 3 shows how DIC counter differs from the previous RTC counter, but still accomplishes the same basic counting function. This figure also uses experimental data to show that the RTC three-counter can count when given three pulses, and also count when pulses are varied in length and interval.
____________________________
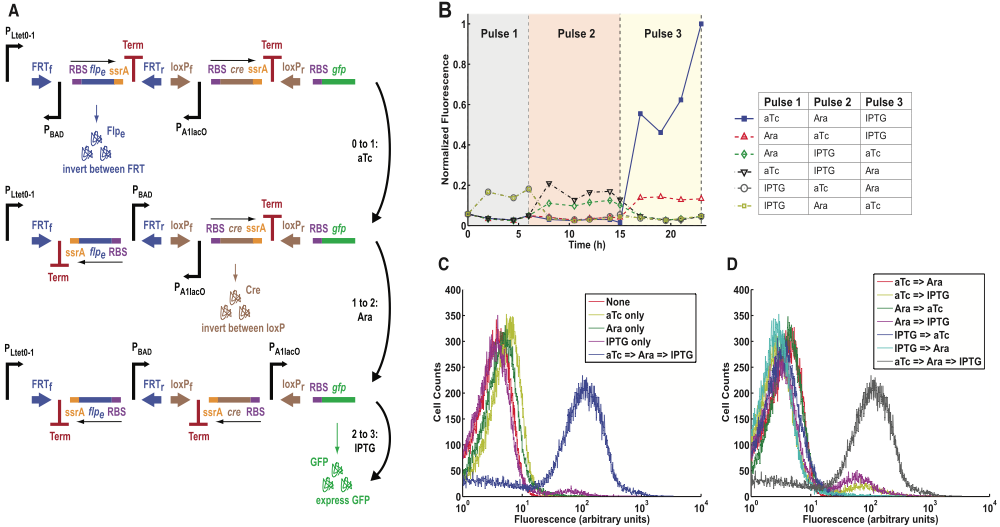
Figure 4 describes a DIC three-counter very similar to the DIC three-counter in figure 3, except that each of the three promoters for each module is activated by a unique inducer (aTc, arabinose, and IPTG), not by one inducer (arabinose).
Figure 4a shows the DIC three-counter circuit model and how it counts to three. After the first pulse of aTc, the first promoter PLtet0-1 upstream of the first module becomes activated, which allows PLtet0-1 to facilitate transcription of the first module. Eventually, translation of the first module produces Flpe recombinase that binds to FRTf and FRTr recombinase recognition sites, which inverts the first module between FRTf and FRTr. As a result, the previously inverted PBAD promoter is now in the right location and direction for second module transcription. The second pulse consists of arabinose, which activates the PBAD promoter in the first module, and thus PBAD facilitates transcription of the second module. Eventually, translation of the third module produces Cre recombinase that binds to loxPf and loxPr recombinase recognition sites, which inverts the second module between loxPf and loxPr. As a result, the previously inverted PA1lacO in the second module is now in the right location and direction for third module transcription. The third pulse consists of IPTG, which activates the PA1lacO promoter in the second module, and thus PA1lacO facilitates the transcription of the third module. Eventually, translation of the third module produces GFP. The third count is verified by measuring increased fluorescence expression due to GFP production during the third pulse.
Figure 4b shows flow cytometry data of DIC three-counter cell populations that have been given three pulses, but the order in which the three inducers (aTc, arabinose and IPTG) were given varied in each treatment. Each line represented the mean fluorescence results of cell populations that were exposed to each type of pulse treatment. Normalized fluorescence is plotted as a function of time, with the three colored vertical sectors representing each pulse.
The only notable increase in fluorescence occurred in cells that were exposed to aTc in the first pulse, arabinose in the second pulse, and IPTG in the third pulse (dark blue line with squares). These dark blue line cells had increased fluorescence only during the third pulse, which is expected when the inducers are given in the order of aTc, arabinose, and IPTG. Inducers given in the correct order results in the counter modules being transcribed/translated in the correct order and the correct promoters for the next module being inverted to the right direction, eventually resulting in GFP production in the third count. In contrast, the rest of the cell populations receiving a different order of aTc, arabinose, and IPTG in their three pulses showed basically no fluorescence increase during the third pulse. Because these cells are not given the correct inducers in the correct order, so the correct modules are not transcribed/translated at the right time and the promoters may still be inverted in the wrong direction. As a result of the DIC three-counter not being able to count to three as intended, GFP production should not increase in the third pulse. The little increases in fluorescence in these cells that should not have high GFP production is attributed to leakage. These results show that only if particular inducers are given in a particular order will the three-counter be able to count to three, resulting in GFP production and higher fluorescence.
Figure 4c shows flow cytometry data with cell counts on the y-axis and fluorescence on the x-axis. Each of the color-coded lines represents cell populations subjected to particular treatments. The red line represents the control, which should show the background fluorescence rate since there was no inducer given to these cells. The three lines representing cell populations that received only one type of inducer (either aTc, arabinose, or IPTG) are very close to the control line (lines toward the left), indicating that there was not much increase in fluorescence in these cells receiving only one inducer. If only one pulse consisting of one inducer is given, the DIC three-counter will not have enough inducers to activate each promoter, produce proteins of interest, and invert modules so promoters face the right direction; therefore, there should never be GFP production in these cells. In contrast, the blue line representing cells receiving the correct order of all three inducers in three pulses has increased fluorescence (line shifted towards the right) relative to the control and cells receiving only one inducer. Because all three inducers are given in the correct order, the DIC three-counter is able to proceed through the sequence of events in order to produce GFP (which verifies that the counter counts to three).
Figure 4d is similar to figure 4c in showing flow cytometry data, except that cells given three inducers in the correct order are being compared to cells given only two inducers. The cells given different combinations of two inducers have lower fluorescence (lines toward the left) relative to the cells given all three inducers in the correct order, which had relatively higher fluorescence (grey line towards the right). Similar to the reasoning given in figure 4c, cells receiving only two inducers do not have enough inducer and/or not in the correct order to activate each promoter, produce proteins of interest, and invert the necessary modules so promoters face the right direction, so there should be no GFP production. Only cells having three inducers given in the correct order can have the DIC three-counter count to three (indicated by more GFP production).
Both figures 4c and 4d demonstrate that DIC three-counter cells receiving less than three inducers and/or incorrect ordering of inducers will not be able to have as much GFP production compared to DIC three-counter cells receiving three inducers in the correct pulse order.
Overall, figure 4 shows that by adding another level of variation and specificity to the synthetic counter model, the authors demonstrate that the counter model can be versatile and specific in counting. Experimentally determination shows that these DIC three-counter can properly count, and that each count can be initiated by specific inducers.
____________________________
Reference
Friedland AE, Lu TK, Wang X, Shi D, Church G, and Collins, JJ. Synthetic Gene Networks That Count. Science. 2009; 324: 1199-1202. <http://bio.davidson.edu/courses/genomics/2011/Bio309_papers/Counting_Network.pdf>.
Genomics Page
Biology Home Page
Davidson College Home Page
Email Questions or Comments to alsu@davidson.edu
© Copyright 2011 Department of Biology, Davidson College, Davidson, NC 28035